Quadrado perfeito

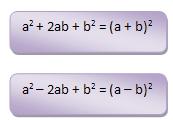
a) O quadrado da soma de duas parcelas [(a + b)2] é igual ao quadrado da primeira parcela [a2], mais o dobro do produto das duas parcelas [2ab], mais o quadrado da segunda parcela [b2].

b) O quadrado da diferença entre duas parcelas [(a – b)2] é igual ao quadrado da primeira parcela [a2], menos o dobro do produto das duas parcelas [2ab], mais o quadrado da segunda parcela [b2].


Justificativa:

c) Observação

Cuidado para não confundir o quadrado da diferença, que é a (a – b)2, com a diferença entre quadrados, que é a2 – b2.

d) Exemplos

a2 + 4a + 4 = a2 + 2 . a . 2 + 22 = (a + 2)2

4a2 + 4ab + b2 = (2a)2 + 2 . 2a . b + b2 = (2a + b)2

36 – 12x + x2 = 62 – 2 . 6 . x + x2 = (6 – x) 2

Nay F.

O Número Mágico

Muitos falam de números. Vocês sabiam que existe um número mágico? Qual seria ele?

Este número para ser formado, faz-se necessário o uso de algumas propriedades:

I- Escolha qualquer número com três algarismos distintos;

II-Escreva esse número de trás para frente;

III- subtraia o menor do maior;

IIII-Inverta também esse resultado e faça a soma

Vejamos alguns exemplos que provam que realmente ele é mágico!

Exemplo 1:

Propriedade I

Número 100

Propriedade II

Número 001   

Propriedade III

100-001 = 099   

Propriedade IIII

990+099 = 1089

Exemplo 2:

Propriedade I

Número 123

Propriedade II

Número 321  

Propriedade III

321-123 =   198

Propriedade IIII

891+198 = 1089

Atenção: Mas atenção, caso o número de três dígitos seja um palíndromo, então não funciona! Números palíndromos são números que se lidos de trás para frente são iguais, assim o resultado obtido na subtração é igual a ZERO, exemplo: 323 - 323 = 0 ou 010-010 = 0.

Valeu! Até a próxima!!!

Bruno e Thiago

Números capicua

Você sabe o que são números capicua ?

Um número é capicua quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo 77, 434, 6446, 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua, como por exemplo:

Partindo do número 84: 84+48=132;132+231=363, que é um número capicua.

Nay F.

Números amigáveis

Você sabe o que são números amigáveis ?

Números amigos são dois números que estão ligados um ao outro por uma propriedade especial: cada um deles é a soma dos divisores do outro. (Um divisor de um número natural são os algarismos que dividem o número em partes exatamente iguais. Os divisores de 6, por exemplo, são 1, 2 e 3.) O menor par de números amigos é (220, 284). Os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284; e os divisores de 284 são 1, 2, 4, 71 e 142, cuja soma é 220. Os números amigos eram conhecidos pelos Pitagóricos, que acreditavam que eles possuíam propriedades místicas e também são consoantes.

Nay F.

O Poder do "4"

Você sabia que é possível obter qualquer número inteiro de 0 a 100 utilizando quatro numerais 4 e sinais de operações matemáticas, como soma, divisão, exponenciação ou fatorial.

Exemplo: Para obter um “3”: É só fazer a seguinte operação: (4+4+4)/4.

E assim sucessivamente.

A imagem abaixo mostra a sequencia !

Essa característica foi descoberta por Malba Tahan e citada no livro O Homem Que Calculava

Segundo o autor é possível escrever, com quatro quatros, todos os números naturais de 0 a 100.

Israel Cardoso

ESTICADORES DE CORDAS

No inicio, por volta de 1000 a.C, no antigo Egito, alguns agricultores foram privilegiados, por habitar nas margens do rio Nilo.  No entanto, havia um problema, na cheia do rio eles tinham que mudar, fazendo-se necessário remarcar as terras, quando o rio baixava, eles voltavam para as antigas terras, e novamente fazia-se necessário remarcar os terrenos; com isso surge os conhecidos esticadores de cordas. 

A necessidade desses trabalhadores era fundamental, pois por meio das medições que eles faziam, determinava o valor que deviam pagar como impostos ao rei Sesóstris.

                                                        

                                                                                 JCarlos

Infinito absoluto

A origem do infinito na matemática deu-se por origem por Georg Ferdinand Ludwig Philipp Cantor ( Matemático Russo, nascido no império Russo - São Petersburgo, 3 de março de 1845 — Halle, 6 de janeiro de 1918), ficou popular por desenvolver a Teoria dos conjuntos (sistema que estuda conjuntos e coleções de elementos ), que a partir deste chegou ao conceito de números transfinitos.

Ferdinand chegou as conclusões que os conjuntos dos números naturais Q é (e)numerável (Algo que se pode enumerar/alterar), e que o conjunto dos números Reais IR é Continuo (Maior que o anterior). Desenvolvendo um paradoxo de uso dos conjuntos afim de provar (Sem sucesso) o conceito de "hipótese do contínuo" que demonstrava a inexistência dos conjuntos de potência intermédia entre os numeráveis e os contínuos.

Devido a problemas psicológicos Georg Ferdinand Ludwig Philipp Cantor paralisou o avanço sobre os conjuntos de números transfinitos. E só então após a descoberta de Paradoxo de Russell (Elaborado por Bertrand Russell - Antigo filosofo matemático do seculo XX ) que contrariava os estudos dos conjuntos  feitos por  Ferdinand , esta contradição agravou o seus problemas psicológicos dificultando cada vez o avanço de pesquisa sobre suas teorias.

Por essa razão começou a se interessar por literatura e religião e foi exatamente nesses estudos que desenvolveu o Infinito Absoluto, que equaciona o infinito como Deus.

Nay & Rael.

Números Negativos

Quem são eles? Por quê negativo?

Quais os primeiros a pensar nos números negativos?

Como desenvolveram a ideia?

Como são conhecidos hoje?

Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.

          

A primeira referência histórica a números negativos ocorre num livro chinês cuja forma mais antiga data da Dinastia Han (202 a.C. - 220 a.C.)

Os números negativos são chamados hoje de números simétricos ou opostos

Os números Negativos na Índia

Os números negativos surgiram com a necessidade de contar as coisas, como os objetos e outras coisas que se havia a necessidade.

Na Índia os esses números foram descobertos quando os matemáticos buscavam algo como referencial para resolver as equações quadráticas. Os números negativos foi utilizado pela 1° vez na obra de "Brahomagupta". Neste país, o número ficou bastante conhecido na época, quando se tratava de dívidas nas escolas.

http://www.somatematica.com.br/negativos.php

 

JC e B.Oliveira