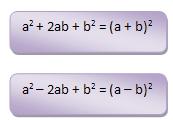trabalho sobre sistema Winplot

Winplot, é um software de matemática dinâmica;  utilizado com diversas finalidades porem seu uso no ensino das escolas é fundamentado para o aprendizado da geometria, álgebra e cálculo.  

o sistema permite construir pontos, figuras geométricas, segmentos, retas, vetores, cónicas e também gráficos de funções, gráficos 2D e 3D; Oferece um conjunto próprio de análise matemática, para identificar pontos de uma função, como raízes ou extremos, tambem permite introduzir equações e coordenadas. Pode ser usado em todos os níveis educacionais e possui recursos que variam de uma simples função de 1 º grau, até funções do 3ºgrau e integrais de todos os tipos. 

É um ótimo plotador de gráficos e uma exelente ferramenta de trabalho.

O sistema foi usado para demonstrar a figura abaixo com seus recusos :

Texto: Recursos tecnológicos em sala de aula

O elo entre o aluno e aprendizagem

Não há nenhuma dúvida que a geração atual e a vindoura irão cada vez mais serem adaptas aos recursos tecnológicos. Com isso na área da educação está diretamente ligada a isso, pois ela permite ao professor trazer aulas mais dinâmicas e divertidas. Esses recursos tecnológicos estão sendo embutidos no ambiente estudantil, desde as escolas como também nas Universidades.

Existem diversos equipamentos e materiais que servem para tornar tais aulas mais interessantes, como o uso de aparelhos digitais, sistemas matemáticos, entre outros recursos.

Essa tecnologia permitiu que houvesse maior interesse e participação por parte dos alunos, pois os alunos compreendem melhor quando eles visualizam aquilo que os professores falam. Estes recursos tem sido um grande aliado dos professores na hora de transmitir o ensino, através de explicações ou atividades em sala de aula.

Ao mesmo tempo que tais recursos digitais são aliados, estão embutidos também as dificuldades. Uma das mais frequentes está  relacionada à distração que esses recursos podem causar nos alunos. No entanto, a tecnologia só atrapalha de fato quem não souber fazer bom uso dela. 

TECNOLOGIA E EDUCAÇÃO

UMA RELAÇÃO  INDISPENSÁVEL NOS DIAS ATUAIS

        Toda novidade é boa, principalmente aquela que acrescenta. O blog ou site, mostraram-se ferramentas sensacionais; nas quais podemos desenvolver competências sistêmicas, de forma simples e objetiva. O fato de ampliar o leque de ferramentas, também possibilita o amadorecimento dos nossos conhecimentos e habilidades, por isso é importantíssimo não desprezar qualquer que seja a opção para nos aprimorar, portanto uma boa atitude para novidade se mostra sempre excelente para o nosso amadorecimento profissional.

A internet tem fascinado os alunos, mesmo com proibições governamentais para o celular, poucos são os alunos que não fazem uso do mesmo em sala de aula, por isso, o recurso tecnológico tem fundamental importância, com possibilidades de atingir este aluno que está apegado à tecnologia, abrindo portas para o aprendizado.

                                                                                                                       
                                                                                                                                          J.Carlos

Benefícios pedagógicos da utilização do blog

As práticas pedagógicas tradicionais não são mais suficientes, visto que as transformações tecnológicas invadem todos os espaços da sociedade. Crianças, adolescentes e jovens estão cada vez envolvidos com as novas tecnologias o que, de fato, os afasta da escola tradicional. Não há mais como negar que as tecnologias devem ser inseridas no contexto escolar, a fim de qualificar e tornar mais significativo o processo de ensino-aprendizagem. Nesse contexto utilizamos uma ferramenta que pode ser usando tanto em sala de aula como fora, o blog. O blog é um espaço de interação e construção do conhecimento, principalmente através da publicação de posts e dos comentários. Estimula a busca pela informação e pela leitura dessa informação, que pode ser transformada em conhecimento pelo aluno, se bem orientado pelo professor. Se torna uma extensão da sala de aula, onde o professor posta links interessantes que podem complementar a matéria e estimular o aluno a comentar sobre tópicos destacados nos textos dos links postados. O aprendizado deixa de ser associado, pelo aluno, a escola, professor, horário rígido, regras e se torna divertido, o que pode estimular o aluno a construir seu conhecimento.

Nay F.

Texto : Experiencia e Impressões de trabalhar com recursos Pedagógicos.

A busca de conhecimento e interação foram fundamentais na criação dos blogs solicitados pela professora.

A experiencia exigida foi a origem de diversas ideias para construção cognitiva, talvez o grande desafio foi desenvolver algo que fosse intuitivo e educativo para as pessoas / alunos.

Aprendi que a educação não é algo simples, requer muita paciência e olhando de forma profunda pode se perceber que é um trabalho enorme e que poucos dão importância.

Quando começamos a publicar as ideias no blog, fiquei imaginando se conseguiria apresentar temas favoráveis e de fácil compreensão, foi uma tarefa difícil, mas busquei aperfeiçoar as ideias e deixa-las de forma "atrativas" para ser um tema no sistema virtual.

Para uma excelente didática os profissionais precisam ser capacitados, e que eles tenham equipamentos com recursos pedagógicos adequados com apoio de profissionais especializados.
O recurso pedagógico adaptado permite que o aluno encontre meios para interagir socialmente, primeiramente dentro da escola na qual ele está inserido, e depois na sociedade da qual ele faz parte.
As ideias elaboradas também criam em mim uma didática pessoal, pois por mais que a gente acumule conhecimento nunca será o bastante ou o suficiente, ter a tecnologia ao lado para educação foi uma mão na roda para mudanças no sistema educacional, aproximando o aluno de sua realidade e, assim, fazendo com que o mesmo contribua para sua aprendizagem ao apresentar os estímulos recebidos através do recurso aplicado.

Israel Cardoso Dos Santos Ramos

PHI

A constante, cuja aproximação numérica é 1,618 é muito importante na arte. O PHI, também chamada de Divina Proporção, parece estar presente em quase todas as proporções dimensionais da natureza e é de grande auxílio aos artistas plásticos eu buscam o realismo em suas obras. Veja alguns exemplos. Ao dividir o número de abelhas fêmeas pelo número de zangões em qualquer colmeia, o resultado será sempre 1,618. Dividindo a distância que vai do alto da cabeça até o chão, depois dividir o resultado pela distância do umbigo até o chão, vai obter 1,618 novamente. A distância de um ombro até a ponta dos dedos dividido pela distância entre o cotovelo até a ponta dos dedos. PHI, 1,618.

Nay F.

Quadrado perfeito

a) O quadrado da soma de duas parcelas [(a + b)2] é igual ao quadrado da primeira parcela [a2], mais o dobro do produto das duas parcelas [2ab], mais o quadrado da segunda parcela [b2].

b) O quadrado da diferença entre duas parcelas [(a – b)2] é igual ao quadrado da primeira parcela [a2], menos o dobro do produto das duas parcelas [2ab], mais o quadrado da segunda parcela [b2].


Justificativa:

c) Observação

Cuidado para não confundir o quadrado da diferença, que é a (a – b)2, com a diferença entre quadrados, que é a2 – b2.

d) Exemplos

a2 + 4a + 4 = a2 + 2 . a . 2 + 22 = (a + 2)2

4a2 + 4ab + b2 = (2a)2 + 2 . 2a . b + b2 = (2a + b)2

36 – 12x + x2 = 62 – 2 . 6 . x + x2 = (6 – x) 2

Nay F.

O Número Mágico

Muitos falam de números. Vocês sabiam que existe um número mágico? Qual seria ele?

Este número para ser formado, faz-se necessário o uso de algumas propriedades:

I- Escolha qualquer número com três algarismos distintos;

II-Escreva esse número de trás para frente;

III- subtraia o menor do maior;

IIII-Inverta também esse resultado e faça a soma

Vejamos alguns exemplos que provam que realmente ele é mágico!

Exemplo 1:

Propriedade I

Número 100

Propriedade II

Número 001   

Propriedade III

100-001 = 099   

Propriedade IIII

990+099 = 1089

Exemplo 2:

Propriedade I

Número 123

Propriedade II

Número 321  

Propriedade III

321-123 =   198

Propriedade IIII

891+198 = 1089

Atenção: Mas atenção, caso o número de três dígitos seja um palíndromo, então não funciona! Números palíndromos são números que se lidos de trás para frente são iguais, assim o resultado obtido na subtração é igual a ZERO, exemplo: 323 - 323 = 0 ou 010-010 = 0.

Valeu! Até a próxima!!!

Bruno e Thiago

Números capicua

Você sabe o que são números capicua ?

Um número é capicua quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo 77, 434, 6446, 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua, como por exemplo:

Partindo do número 84: 84+48=132;132+231=363, que é um número capicua.

Nay F.

Números amigáveis

Você sabe o que são números amigáveis ?

Números amigos são dois números que estão ligados um ao outro por uma propriedade especial: cada um deles é a soma dos divisores do outro. (Um divisor de um número natural são os algarismos que dividem o número em partes exatamente iguais. Os divisores de 6, por exemplo, são 1, 2 e 3.) O menor par de números amigos é (220, 284). Os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284; e os divisores de 284 são 1, 2, 4, 71 e 142, cuja soma é 220. Os números amigos eram conhecidos pelos Pitagóricos, que acreditavam que eles possuíam propriedades místicas e também são consoantes.

Nay F.

O Poder do "4"

Você sabia que é possível obter qualquer número inteiro de 0 a 100 utilizando quatro numerais 4 e sinais de operações matemáticas, como soma, divisão, exponenciação ou fatorial.

Exemplo: Para obter um “3”: É só fazer a seguinte operação: (4+4+4)/4.

E assim sucessivamente.

A imagem abaixo mostra a sequencia !

Essa característica foi descoberta por Malba Tahan e citada no livro O Homem Que Calculava

Segundo o autor é possível escrever, com quatro quatros, todos os números naturais de 0 a 100.

Israel Cardoso

ESTICADORES DE CORDAS

No inicio, por volta de 1000 a.C, no antigo Egito, alguns agricultores foram privilegiados, por habitar nas margens do rio Nilo.  No entanto, havia um problema, na cheia do rio eles tinham que mudar, fazendo-se necessário remarcar as terras, quando o rio baixava, eles voltavam para as antigas terras, e novamente fazia-se necessário remarcar os terrenos; com isso surge os conhecidos esticadores de cordas. 

A necessidade desses trabalhadores era fundamental, pois por meio das medições que eles faziam, determinava o valor que deviam pagar como impostos ao rei Sesóstris.

                                                        

                                                                                 JCarlos

Infinito absoluto

A origem do infinito na matemática deu-se por origem por Georg Ferdinand Ludwig Philipp Cantor ( Matemático Russo, nascido no império Russo - São Petersburgo, 3 de março de 1845 — Halle, 6 de janeiro de 1918), ficou popular por desenvolver a Teoria dos conjuntos (sistema que estuda conjuntos e coleções de elementos ), que a partir deste chegou ao conceito de números transfinitos.

Ferdinand chegou as conclusões que os conjuntos dos números naturais Q é (e)numerável (Algo que se pode enumerar/alterar), e que o conjunto dos números Reais IR é Continuo (Maior que o anterior). Desenvolvendo um paradoxo de uso dos conjuntos afim de provar (Sem sucesso) o conceito de "hipótese do contínuo" que demonstrava a inexistência dos conjuntos de potência intermédia entre os numeráveis e os contínuos.

Devido a problemas psicológicos Georg Ferdinand Ludwig Philipp Cantor paralisou o avanço sobre os conjuntos de números transfinitos. E só então após a descoberta de Paradoxo de Russell (Elaborado por Bertrand Russell - Antigo filosofo matemático do seculo XX ) que contrariava os estudos dos conjuntos  feitos por  Ferdinand , esta contradição agravou o seus problemas psicológicos dificultando cada vez o avanço de pesquisa sobre suas teorias.

Por essa razão começou a se interessar por literatura e religião e foi exatamente nesses estudos que desenvolveu o Infinito Absoluto, que equaciona o infinito como Deus.

Nay & Rael.

Números Negativos

Quem são eles? Por quê negativo?

Quais os primeiros a pensar nos números negativos?

Como desenvolveram a ideia?

Como são conhecidos hoje?

Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.

          

A primeira referência histórica a números negativos ocorre num livro chinês cuja forma mais antiga data da Dinastia Han (202 a.C. - 220 a.C.)

Os números negativos são chamados hoje de números simétricos ou opostos

Os números Negativos na Índia

Os números negativos surgiram com a necessidade de contar as coisas, como os objetos e outras coisas que se havia a necessidade.

Na Índia os esses números foram descobertos quando os matemáticos buscavam algo como referencial para resolver as equações quadráticas. Os números negativos foi utilizado pela 1° vez na obra de "Brahomagupta". Neste país, o número ficou bastante conhecido na época, quando se tratava de dívidas nas escolas.

http://www.somatematica.com.br/negativos.php

 

JC e B.Oliveira

Eaí galera, tudo bom com vocês?
Esse aí é nosso blog,  para falarmos de matemática, só que utilizando uma linguagem informal.

Vamos lá? O 0 (zero) é interessante pois ele  é diferente quanto aos demais números,
Às vezes esquecemos por alguns momentos que ele existe,
O número 0 (zero) está ligado a nossa mente com ideia de nada, exemplo: Ninguém compra 0 biscoito pra comer.

Bruno e Thiago

A origem do zero

De onde veio o zero?

O zero surge inicialmente entre os babilônios, hindus e os maias.

Qual a importância do zero?

Para indicar a ideia do nada.

Por que zero?

Para representar o nada.

O número zero, surgiu em três povos:

Babilônios: Civilização antiga que não possuía conceito sobre o número zero, mesmo com a ideia do número utilizavam o espaço vago, somente mais tarde foi criado um símbolo  para representação do mesmo.

Hindus: Civilização que utilizava o sistema de numeração decimal (O mesmo que utilizamos hoje 0,1,2,3,4...) criaram um símbolo para representar o vazio chamada de SUNYA).

Maias: Civilização que para representar o número zero utilizava o desenho de uma concha.

Reparem que todas as três civilizações possuíam conhecimento sobre o número zero, hoje já muito utilizado, foi desenvolvido com ponto de partida do conhecimento desses antigos povoados.

A partir da idade média na Europa, devido a aceitação dos algarismos arábicos divulgados por Leonardo Fibonacci (Matemático italiano) que ficou conhecido pela descoberta da (Sequência de Fibonacci).

Na época a representação do número zero gerou um paradoxo, pois muitos não conseguia imaginar a quantificação e representação do nada.

Apesar de difícil compreensão o número zero foi considerado como uma das maiores descobertas da humanidade, criando conceitos matemáticos para cálculos a partir de então.

                                                                                                                 Rael e JC